Cinemàtica.

(dal greco kínema, movimento). Parte della scienza sviluppata in fisica e in meccanica razionale che si occupa del movimento e ne dà la descrizione indipendentemente dalle cause che lo hanno generato. Per lo studio della c. sono necessarie le nozioni di spazio e di tempo che occorre assumere come primitive, appunto per questo la c. viene anche definita come geometria del movimento. La c. si divide in due settori principali: c. del punto materiale, che si occupa del moto dei corpi quando questi ultimi sono identificabili con un punto geometrico e c. dei corpi rigidi, per lo studio della quale è necessaria la definizione di corpo rigido, che è la seguente: un corpo si considera rigido se è invariabile la distanza fra due punti qualsiasi di esso (se tale distanza fosse variabile, anche di pochissimo, il corpo sarebbe elastico). Lo studio del movimento, quindi lo studio della c. del punto materiale e/o dei corpi rigidi, può essere effettuato soltanto se si prende come base un sistema di riferimento costituito ad esempio da un sistema di assi cartesiani bi o tri-dimensionali a seconda che il moto sia piano o spaziale. Quando il moto è riferito allo spazio celeste, prendendo come base di riferimento il sistema delle stelle fisse, il moto viene detto assoluto, quando si ha un sistema di riferimento che si muove rispetto al sistema delle stelle fisse, preso come assoluto, il moto viene chiamato relativo. Per individuare il moto di un corpo occorre individuare il moto dei vari punti; il moto diventa noto quando se ne conosce la forma geometrica o l'espressione matematica della traiettoria insieme alla legge che esprime lo spazio percorso dal mobile in funzione del tempo: dx/dt (legge oraria). Daremo ora una breve descrizione dei principali tipi di moto studiati dalla c.
║ Moto uniforme: è il tipico moto di un corpo che percorre spazi uguali in tempi uguali, comunque piccoli, vengano considerati sia gli spazi sia i tempi. Da questo tipo di moto è facile dedurre la definizione di velocità come spazio percorso nell'unità di tempo. La velocità in un tipo qualsiasi di moto si può considerare sotto diverse definizioni e precisamente: velocità istantanea, velocità media, velocità massima; in questo tipo di moto tutte queste velocità coincidono, infatti si dice moto uniforme appunto perché la velocità è costante. Se si considera un intervallo di tempo molto piccolo, al limite infinitesimo, entro il quale si esamina il moto e si considera la derivata dello spazio fatta rispetto al tempo. tale derivata ci dà la velocità istantanea.
║ Moto uniformemente vario: è quel tipo di moto nel quale la velocità varia al trascorrere del tempo, ma proporzionalmente al tempo stesso: la derivata della velocità fatta rispetto al tempo (dv/dt) ci permette di definire la cosiddetta accelerazione, che in questo caso semplice si può anche esprimere come la variazione della velocità nell'unità di tempo, che per questo tipo di moto è costante. L'accelerazione può essere positiva, se il moto è uniformemente accelerato, negativa se il moto e uniformemente ritardato. Le leggi che governano questo tipo di moto si possono esprimere mediante le formule matematiche:



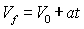
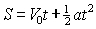
dove i simboli hanno il seguente significato: V_f = velocità raggiunta alla fine del moto (velocità finale); V₀ = velocità iniziale: a = accelerazione: t = tempo. Analizzando queste formule è facile ricavare, quando si voglia frenare un mobile applicandogli un'accelerazione negativa fino ad arrestarlo, lo spazio e il tempo di arresto che risultano:



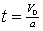
Un caso particolare, ma di notevole interesse, di moto vario, è il cosiddetto moto naturalmente accelerato, che è il moto col quale avviene la caduta dei gravi: esso è caratterizzato da una accelerazione costante nel tempo chiamata g che vale circa 9,81 m al secondo per secondo alla nostra latitudine. ║ Moto circolare: è il moto di un punto che compie una traiettoria circolare di raggio r. In questo tipo di moto vengono definite le seguenti grandezze: velocità tangenziale o periferica che non è altro che il rapporto tra l'arco descritto (ds) e il tempo impiegato a percorrerlo (dt): v = ds/dt; velocità angolare: per definirla occorre considerare il raggio vettore che si muove assieme al punto materiale, esso descriverà l'angolo d 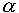mentre il punto descrive l'arco ds; il rapporto tra l'angolo descritto dal raggio vettore e il tempo impiegato a descriverlo prende il nome di velocità angolare e si può scrivere in termini di derivate come 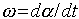(occorre notare che gli angoli vanno sempre espressi in radianti). Se il moto circolare è uniforme l'espressione che lega la velocità angolare a quella periferica e viceversa è la seguente: v = 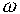r. Se il moto è uniforme si ha come conseguenza di quanto detto prima che: 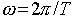, dove 2 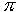è un angolo giro completo e T il tempo impiegato dal raggio vettore (o dal punto materiale) a descrivere un giro completo. T viene detto periodo, mentre il suo inverso f = 1/T viene detto frequenza che non è altro che il numero di giri percorsi nell'unità di tempo. Se la velocità angolare (e di conseguenza quella periferica) è costante si ha il moto circolare uniforme (prima descritto), diversamente il moto risulta caratterizzato da un'accelerazione angolare, che è il rapporto tra la variazione di velocità angolare e il tempo in cui avviene, in termini di derivate: . 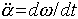Se l'accelerazione angolare è nulla il moto è circolare uniforme, se è costante il moto è uniformemente vario (accelerato o ritardato), se è variabile allora il moto è comunque vario.
║ Moto armonico semplice: è il movimento della proiezione sul diametro di un punto che descrive una circonferenza con moto circolare uniforme. Le caratteristiche principali di questo tipo di moto si possono elencare nel modo seguente: in primo luogo la proiezione che il punto compie sul diametro delle escursioni portandosi da un estremo all'altro un numero indefinito di volte in modo alternativo e in versi opposti; in secondo luogo la velocità si annulla agli estremi del diametro, è massima al centro e cambia direzione e verso a ogni semicirconferenza descritta dal punto; in terzo luogo l'accelerazione è costantemente diretta verso il centro (in cui assume valore nullo) e ha valore massimo agli estremi (come del resto è ovvio essendo l'accelerazione la derivata della velocità fatta rispetto al tempo).
║ Moto centrale: è quel tipo di moto di un punto materiale nel quale l'accelerazione è costantemente diretta verso un punto chiamato centro del moto. La caratteristica principale di questo tipo di moto è che in esso risulta costante il rapporto tra la velocità areolare e il tempo impiegato a descriverla (con velocità areolare s'intende l'area descritta dal raggio vettore che collega il centro del moto al punto materiale).
║ Moto Kepleriano: questo moto è un tipo particolare di moto centrale studiato da Keplero, è descritto e definito dalle leggi enunciate da questo grande fisico, ed è il tipico moto dei pianeti che girano attorno al sole.
║ Moto elastico: questo tipo di movimento, che è un altro esempio notevole di moto centrale, studia le vibrazioni di un corpo elastico una volta che quest'ultimo sia leggermente deformato. quindi lasciato successivamente libero a sé.
║ Moto elicoidale uniforme: questo è un moto non di tipo piano (come quelli fin ora descritti), bensì di tipo spaziale, ed è precisamente quello descritto da un corpo che descrive una traiettoria ad elica cilindrica; si può considerare come un moto composto di due moti piani ortogonali e precisamente: di un moto di traslazione rettilineo uniforme e di un moto circolare uniforme. "composizione di movimenti": questa parte della c. basata sulla legge di Galileo che dice "se un punto materiale è soggetto a più movimenti e ognuno di questi avviene in modo indipendente dagli altri, alla fine di un certo tempo il punto occupa quella stessa posizione in cui si troverebbe se i movimenti avvenissero successivamente (e non contemporaneamente) e per lo stesso tempo", ci permette di studiare il movimento di un corpo che si muove secondo le leggi più diverse, come una composizione dei moti elementari descritti precedentemente. Dalla legge di Galileo discendono facili considerazioni e corollari, come ad esempio quelli che ci permettono di dedurre che: la velocità risultante di una serie di moti, è sempre la somma vettoriale delle velocità componenti; il moto risultante è rettilineo uniforme se i moti componenti sono rettilinei uniformi: il moto risultante è accelerato uniforme se i moti componenti sono rettilinei uniformi; il moto risultante è accelerato uniforme se tali sono i moti componenti; e così via. Di più recente studio è la cosiddetta c. relativistica, che si basa sulla teoria della relatività di Einstein.