È immediata l'estensione a figure che si possono considerare come somma o differenza di trapezoidi, per le quali il calcolo dell'a. (o quadratura, come si dice talvolta) si riduce a più integrali definiti, e successivamente alla somma algebrica dei risultati. Spesso il calcolo delle a. di figure piane è semplificato mediante un passaggio dalle coordinate cartesiane ad altri sistemi di coordinate, come ad esempio, le coordinate polari. In un tale sistema, detto ρ raggio vettore e detta θ l'anomalia, l'a. del settore definito dalle disuguaglianze:
θ' ≤ θ ≤ θ''; ≤ ρ ≤ ρ (θ)
è data da:
Ad esempio calcoliamo l'a. del cerchio, che è definito in coordinate polari dalla relazione ρ = cost. = R (raggio della circonferenza) per tutti i 360 ° dell'angolo ρ (anomalia):
che è il risultato ben noto. Nel caso in cui la superficie da quadrare non sia riducibile in modo semplice a una somma (algebrica) di trapezoidi nemmeno col passaggio a coordinate polari, l'a. A è ancora calcolabile mediante un integrale doppio. Sia R la superficie da integrare (o campo di integrazione) allora:
Ricordiamo che l'integrale doppio scritto sopra può sempre ridursi (sotto ipotesi assai poco restrittive) a due successive integrazioni, rispetto alla x e poi alla y o viceversa. Infatti il campo R o è della forma tale che soddisfa le disuguaglianze:
a ≤ x ≤ b; f(x) ≤ y ≤ g(x)
(col che la f(x) e la g(x) rappresentano i confini di R), oppure si può suddividere a disuguaglianze di tale tipo. Supponiamo di essere nel primo caso (il secondo è perfettamente analogo, solo che si devono integrare i vari settori e infine sommare). Allora:
onde il calcolo dell'integrale doppio è ridotto all'integrazione in y fra limiti variabili, seguita dall'integrazione in x. L'a. del campo R nel piano può anche essere calcolata come integrale di linea. Infatti detto C il contorno di R, il teorema di Gauss-Green ci permette di ricavare la seguente uguaglianza:
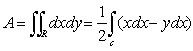
Esistono molti metodi per il calcolo approssimato delle superfici, sia numerici che grafici. Ne diamo solo un breve cenno. Ci riferiamo a un trapezoide definito dalla curva y = f(x) con a ≤ x ≤ b, f(x) ≥ 0 in tutto l'intervallo (a, b) oltre che continua in tale intervallo. Si suddivida l'intervallo (a, b) in n parti uguali di lunghezza h = (b-a)/n. L'a. è data da:
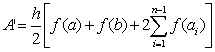
essendo ai il generico estremo degli intervalli (a0, a1), (a1, a2), ... (an-1, b) di lunghezza h in cui è stato diviso (a,b). La formula riportata si dice di Bèzout o dei trapezi in quanto l'a. si ottiene come somma di n trapezi definiti dalle coordinate dei vertici:
(ai, 0); [ai, f(ai)];
[ai+1, f(ai+1)]; (ai+1, 0)
al posto dei trapezoidi:
ai ≤ x ≤ai+1; 0 ≤ y ≤ f(x)
L'a. A' così ottenuta sarà tanto più vicina all'a. vera A quanto più grande è n; A' è approssimato per eccesso se la curva volge la concavità verso l'alto, per difetto se la volge verso il basso. Un'altra formula è quella di Simpson. Suddiviso l'intervallo (a,b) in n parti uguali (con n pari) sia yi = f(ai) con i = 0, 1, 2, ... n il valore assunto dalla funzione in corrispondenza alla generica suddivisione. Evidentemente y0 = f(a) e yn = f(b). Allora l'a. detto di solito h = (b-a)/n_, è data da:
Con la stessa suddivisione, ma n qualsiasi, si può applicare la regola di Weddle o dei tre ottavi:
Ovviamente anche in questi casi la precisione è tanto più elevata quanto maggiore è n. Per quanto concerne le integrazioni grafiche, esse sono tutte basate su una serie di costruzioni che si possono eseguire con la sola squadra (o con l'ausilio del compasso), al termine delle quali un segmento è uguale alla misura dell'a. della superficie considerata, in una scala che è data dal prodotto delle scale usate per le ascisse e le ordinate e la lunghezza di un segmento. Sostanzialmente tali costruzioni sono ancora basate sulla divisione della superficie in tanti trapezoidi, e sulla loro sostituzione con trapezi o rettangoli, e sono quindi approssimate. Sono però molto pratiche, onde si usano spesso in molti campi della tecnica (ingegneria civile e meccanica, ecc.). Per le superfici, il problema della loro quadratura è meno semplice. Sia data una funzione f(x, y) definita in un certo campo R del piano x, y. Considerata la superficie z = f(x, y) nello spazio, si pongono due problemi: come definire la sua a. e come calcolarla. Come già si definiva l'a. del cerchio, come limite comune cui tendono l'a. del poligono regolare inscritto e circoscritto al tendere all'infinito del loro numero di lati (quando i lati dei due poligoni siano paralleli), così l'a. di una superficie è definita come limite delle superfici di due poliedri (inscritto e circoscritto); va tuttavia ricordato che non tutte le superfici sono quadrabili; almeno in certi campi. Un procedimento per stabilire se la superficie è ad a. finita (cioè quadrabile) risale a Leonida Tonelli (1926) e consiste nel vedere se un poliedro a superfici triangolari inscritto nella superficie, possiede un'a. che tende a un limite finito al tendere a zero del massimo dei suoi lati. Stabilita dunque la possibilità di quadrare una superficie, se la f(x,y) è continua con le sue derivate parziali del primo ordine in tutto il campo R (chiuso, limitato e quadrabile) l'a. A della parte di superficie z = f(x, y) comprende tutti i punti (x, y, z) per cui (x, y) sono in R, è data da:
avendo posto:
Il calcolo è spesso complesso, ma si semplifica nel caso di superfici di rotazione (che supporremo di rotazione attorno all'asse z). Se allora z = g(x) è l'equazione della curva mediana, questa è data da:
Passando a coordinate polari può essere semplificata in modo da ridurre l'integrale doppio a un integrale semplice. Infatti la relazione precedente si può trasformare nella:
ove r è il raggio della proiezione sul piano x, y della parte di superficie di cui si calcola l'a., mentre gli altri simboli hanno il significato solito. • Fis. - Legge delle a.: legge formulata nel 1609 da Keplero sul moto dei pianeti: le a. descritte dal segmento di retta che congiunge il pianeta col sole (raggio vettore) sono proporzionali al tempo impiegato a descriverle. ║ Teorema delle a.: se M è un punto generico di un sistema in movimento, riferito a una terna di assi x, y, z di riferimento, con origine in O, vale la proposizione: il momento rispetto a O della velocità dt/ds del punto mobile M è uguale al doppio della derivata, eseguita rispetto al tempo, dell'a. dA descritta dal raggio vettore OM. Se le forze esterne presentano momento nullo rispetto a una retta fissa vale la proposizione: la somma dei prodotti delle singole masse per le proiezioni sul piano normale alla retta, delle a. descritte dai raggi vettori che da un punto qualunque della retta vanno alle masse stesse, varia proporzionalmente al tempo. Se le forze esterne presentano momento nullo rispetto a un punto fisso, si ha che la somma dei prodotti delle singole masse per le a. descritte dai raggi vettori che da quel punto vanno alle masse stesse, varia proporzionalmente al tempo. Se le forze esterne sono nulle e il sistema inizialmente in quiete si mette in moto per effetto di sole forze interne, vale la proposizione: la somma dei prodotti delle singole masse per le a. descritte dai raggi vettori, che da un punto fisso qualunque vanno alle masse stesse, è sempre nulla. • Anat. - A. corticali: zone della corteccia cerebrale dotate di funzioni differenti da quelle circostanti. Comprendono le a. di proiezione, sede dei punti di arrivo e di partenza delle vie nervose, le a. di associazione, sede di centri nervosi che sovraintendono le attività fisiche o psichiche, le a. soppressorie, in cui si creano inibizioni verso le funzioni di altre zone della corteccia. • Sport - Zona del campo chiaramente segnata sul terreno con linee bianche nei giochi di palla. ║ Nella pallacanestro, la parte prospiciente ciascuno dei due canestri e avente forma trapezoidale con la base maggiore sulla linea di fondo del campo da gioco. L'interno dell'a. è lo spazio in cui viene conteggiata l'infrazione dei tre secondi. Lungo il lato dell'a. opposto al canestro vengono effettuati i tiri liberi. ║ Nel calcio, a. d'angolo: piccola a. di un metro di raggio, situata all'intersecazione delle linee laterali con le linee di fondo, e dalla quale viene tirato il calcio d'angolo. A. del calcio di rigore: porzione di circolo, costituita da un raggio di m 9,15 che, fatto centro nel punto del calcio di rigore, viene tracciata all'esterno dell'a. stessa. L'arbitro deve osservare che i giocatori, al momento del tiro del calcio di rigore, non si trovino all'interno dell'a. del calcio di rigore, ma sostino al di fuori della linea bianca. A. di porta: spazio delimitato da due linee, della lunghezza di 5,50 m ciascuna, perpendicolari alla linea della porta; cominciano sulla linea di fondo alla distanza di 5,50 m da ciascun palo. Le linee perpendicolari sono congiunte da una linea parallela alla linea della porta, in modo da formare un rettangolo. Entro questa a. (e non oltre) viene posto il pallone quando il portiere, o un suo compagno di squadra, deve effettuare il calcio di rinvio. A. di rigore: è delimitata da due linee della lunghezza di 16,50 m, congiunte da una linea parallela alla linea della porta, vengono tracciate a partire dalla linea di fondo, alla distanza di 16,50 m da ciascuno dei pali. L'a. di rigore segna il limite ove il portiere può usare le mani per giocare il pallone. Oltre l'a. di rigore può intervenire soltanto con i piedi, come qualsiasi altro giocatore. Inoltre nell'a. di rigore i falli intenzionali dei difensori effettuati ai danni dei giocatori avversari vengono puniti appunto con il calcio di rigore. ║ Nel rugby, a. dei ventidue: zona del terreno di gioco compresa tra la linea dei ventidue metri e quella di fondo; in pratica l'a. dei ventidue è la parte di terreno antistante la porta. A. di pallone morto: zona del terreno di gioco posta al di là della linea di pallone morto che, raggiunta dal pallone, segna la conclusione dell'azione. A. di meta: zona del terreno di gioco delimitata dalle linee di meta e dalle linee di pallone morto. ║ Nel baseball, a. dello strike: quel rettangolo ideale in cui deve essere lanciata la palla per essere giudicata strike dall'arbitro, avente come base il piatto di casa base e come altezza lo spazio compreso tra la linea delle spalle e le ginocchia del battitore, quando questi assume la sua naturale posizione di battuta. L'arbitro, nel valutare tale zona, dovrà tener conto della posizione abituale del battitore nel momento in cui questo si accinge a battere la palla lanciata. ║ Nella pallavolo, a. di servizio: rettangolo posto esternamente alla linea di fondo, all'estremo vertice destro del terreno di gioco, da dove i giocatori effettuano la battuta. L'a. di servizio è segnata a terra da due linee parallele di 15 cm x 5, una sul prolungamento della linea laterale destra, l'altra a 3 m sulla sinistra della prima; la profondità minima è di 2 m. • Dir. - A. monetaria: ambito geografico e politico in cui è in uso una stessa moneta ovvero in cui è vigente un regime di cambi fissi tra monete diverse. In base ad alcune teorie economiche, l'estensione di un'a. monetaria può essere definita secondo criteri di efficienza economica: quanto maggiore è la mobilità interna dei fattori in rapporto a quella con l'estero e quanto minore è la dipendenza dell'economia interna dell'a. relativamente al mercato estero, tanto meglio sarebbe estendere a quest'ultima un'unica moneta o un insieme di monete a cambio fisso. La CEE, allo scopo di acquistare autonomia all'interno del sistema monetario internazionale ha tentato di creare un'a. monetaria propria, dapprima nel 1972 introducendo il cosiddetto "serpente monetario" e nel 1979 con lo SME. • Edil. - A. fabbricabile: porzione di suolo considerata edificabile, su cui cioè è consentito costruire edifici in base alla legislazione urbanistica vigente. • Dir. - L'insufficienza della legge urbanistica n. 1.150 del 17.8.1942 e la necessità di disporre di una legislazione in grado di sanare la piaga dell'abusivismo edilizio ha costituito per anni materia di dibattito politico, restando al centro di roventi polemiche, prima di giungere a una normativa che, ponendo vincoli e indicando criteri di espansione dei centri urbani, tendesse a favorire una sistemazione razionale del territorio, colpendo inoltre l'abusivismo edilizio e la speculazione consentita dalla valorizzazione dei suoli agricoli confinanti con le a. urbane. Speculazioni e abusivismo, oltre a compromettere lo sviluppo razionale del territorio, hanno consentito per anni di scaricare sulle amministrazioni comunali i costi di urbanizzazione delle a. fabbricabili, ossia a far gravare sulla collettività, sia le opere di urbanizzazione primaria (strade, fognature, acquedotti, reti telefoniche, elettriche, del gas, ecc.), sia le opere di urbanizzazione secondaria (verde pubblico, parcheggi, edifici scolastici). A partire dalla legge 167 del 18.4.1963, tesa a favorire l'acquisizione da parte degli enti pubblici di a. destinate all'edilizia popolare, sono stati presi una serie di provvedimenti legislativi volti a sanare la situazione. Pur essendo stata rimediata la tendenza prevalente all'inizio degli anni Sessanta, di introdurre una normativa basata sul criterio dell'esproprio generalizzato da parte dei comuni, di tutte le a. fabbricabili nell'ambito del loro territorio, in modo da colpire alla radice la speculazione, le norme introdotte tendono a inquadrare in una visione globale tutte le attività del settore urbanistico, sulla base di una legislazione edilizia molto severa (V. EDILIZIA). Con la legge-ponte 6.8.1967, fu sancito l'obbligo per i comuni di impostare piani regolatori e l'obbligo per i lottizzatori privati di convenzionarsi con il comune. Con la legge 22.10.1971 n. 865, venne definita la procedura di indennità di esproprio delle a. fabbricabili da destinarsi all'edilizia popolare e ai servizi, integrando la legge 167 del 1963. Una serie di importanti innovazioni, riguardanti la "disciplina dei suoli", sono state introdotte dalla legge 28.1.1977 n. 210 (nota come "legge Bucalossi", dal nome del suo promotore). Con questa legge, è stato introdotto l'istituto della concessione (V.) che ha sostituito la licenza edilizia. La concessione a edificare prevede l'esborso di un onere, costituito da una quota proporzionale al costo di costruzione e da una quota proporzionale ai costi di urbanizzazione. Le opere di urbanizzazione possono essere eseguite direttamente dal concessionario, oppure il loro costo può venire scontato attraverso un corrispettivo versamento al comune che ha provveduto alla realizzazione delle opere necessarie. La legge fa inoltre obbligo ai comuni di identificare le a. fabbricabili destinate sia all'edilizia pubblica che a quella privata, con possibilità di esproprio delle a. fabbricabili che, alla scadenza dei piani urbanistici predisposti con validità pluriennale, risultassero inutilizzate. Alcune norme riguardanti l'esproprio sono state dichiarate illegittime dalla Corte Costituzionale, con sentenza del 30.1.1980 e modificate dalla legge 20.7.1980 n. 385.
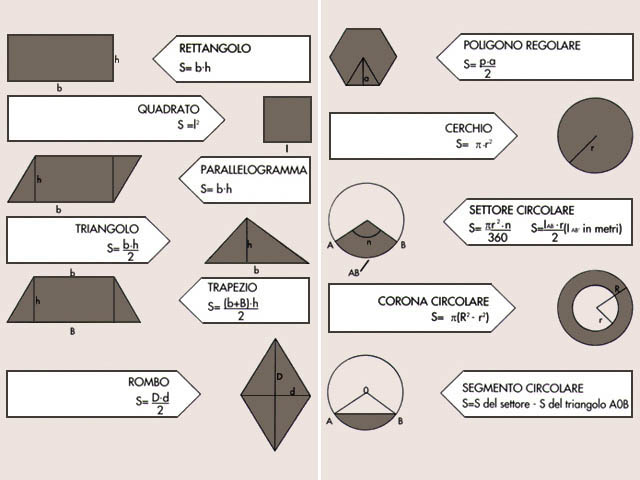
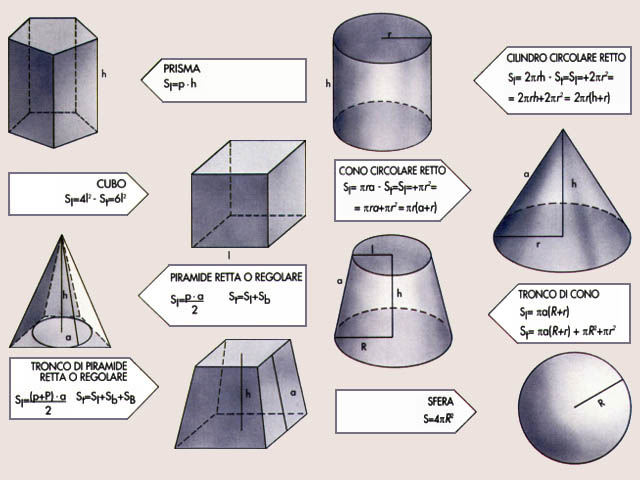
Calcolo dell'area di figure piane
S = superficie; S1 = superficie totale; Sb, SB = superficie di base; l = lato; b,B = base; h = altezza; d,D = diagonale; a = apotema; p,P = perimetro; r,R =raggio; n = ampiezza dell'angolo; lAB = lunghezza dell'arco.
S = superficie; S1 = superficie totale; Sb, SB = superficie di base; l = lato; b,B = base; h = altezza; d,D = diagonale; a = apotema; p,P = perimetro; r,R =raggio; n = ampiezza dell'angolo; lAB = lunghezza dell'arco.